转载自：http://blog.csdn.net/jiaomeng/archive/2007/01/27/1495500.aspx

        Bloom Filter是一种空间效率很高的随机数据结构，它利用位数组很简洁地表示一个集合，并能判断一个元素是否属于 这个集合。Bloom Filter的这种高效是有一定代价的：在判断一个元素是否属于某个集合时，有可能会把不属于这个集合的元素误 认为属于这个集合（false positive）。因此，Bloom Filter不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下，Bloom Filter通过极少的错误换取了存储空间的极大节省。

集合表示和元素查询

下面我们具体来看Bloom Filter是如何用位数组表示集合的。初始状态时，Bloom Filter是一个包含m位的位 数组，每一位都置为0

为了表达S={x₁, x₂,…,x_n}这样一个n个元素 的集合，Bloom Filter使用k个相互独立的哈希函数（Hash Function），它们分别将集合中的每个元素映射到{1,…,m}的范围中。对任意一个元素x，第i个哈希函数映射的位置h_i(x)就会被置为1（1≤i≤k）。注意，如果一个位置多次被置为1，那 么只有第一次会起作用，后面几次将没有任何效果。在下图中，k=3，且有两个哈希函数选中同一 个位置（从左边数第五位）。  

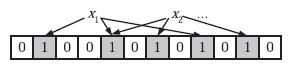
在判断y是否 属于这个集合时，我们对y应用k次哈希函数，如果所有h_i(y)的位置都是1（1≤i≤k），那么我们就认为y是集合 中的元素，否则就认为y不是集合中的元素。下图中y₁就不是集合中的元素。y₂或者属于这个集合，或者刚好是一个false positive。

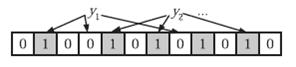
错误率估计

前面我们已经提到了，Bloom Filter在判断一个元素是否属于它表示的集合时会有一定的错误率（false positive rate），下面我们就来估计错误率的大小。在估计之前为了简化模型，我们假设kn<m且各个哈希函数是完全随机的。当集合S={x₁, x₂,…,x_n}的所有元素都被k个哈希 函数映射到m位的位数组中时，这个位数组中某一位还是0的概率是：

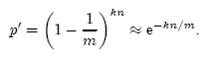
其中1/m表示任意一个哈希函数选中这 一位的概率（前提是哈希函数是完全随机的），(1-1/m)表示哈希一次没有选中这一位 的概率。要把S完全映射到位数组中，需要做kn次哈 希。某一位还是0意味着kn次哈希都没有选中它，因此这 个概率就是（1-1/m）的kn次方。令p = e^-kn/m是为了简化运算，这里用到了计算e时常用的近似：

令ρ为位数组中0的比例，则ρ的数学 期望E(ρ)= p’。在ρ已知的情况 下，要求的错误率（false positive rate）为：

(1-ρ)为位数组中1的比例，(1-ρ)^k就表示k次哈希都刚好选中1的区域，即false positive rate。上式中第二步近似在前面已经提到了，现在来看第一步近似。p’只是ρ的数学期望， 在实际中ρ的值有可能偏离它的数学期望值。M. Mitzenmacher已经证明^[2] ，位数组中0的比例非常集中地分布在它的数学期望值的附近。因此，第一步的近似得以成立。分别将p和p’代入上式中，得：

相比p’和f’，使用p和f通常在分析中更为方便。 

最优的哈希函数个数 

既然Bloom Filter要靠多个哈希函数将集合映射到位数组中，那么应该选择几个哈希函数才能使元素查询时的错误率降到最低 呢？这里有两个互斥的理由：如果哈希函数的个数多，那么在对一个不属于集合的元素进行查询时得到0的概 率就大；但另一方面，如果哈希函数的个数少，那么位数组中的0就多。为了得到最优的哈希函数个 数，我们需要根据上一小节中的错误率公式进行计算。

先用p和f进行计算。注意到f = exp(k ln(1 − e^−kn/m))，我们令g = k ln(1 − e^−kn/m)，只要让g取到最 小，f自然也取到最小。由于p = e^-kn/m，我们可以将g写成

根据对称性法则可以很容易看出当p = 1/2，也就是k = ln2· (m/n)时，g取得最小值。在这种情况下，最小错误率f等于(1/2)^k ≈ (0.6185)^m/n。另外，注意到p是位数组中某一位仍是0的概率，所以p = 1/2对应着位数组中0和1各一半。换句话说，要想保持错误率低，最好让位数组有一半还空着。

需要强调的一点是，p = 1/2时错误率最小这个结果并不依赖于近似值p和f。同样对于f’ = exp(k ln(1 − (1 − 1/m)^kn))，g’ = k ln(1 − (1 − 1/m)^kn)，p’ = (1 − 1/m)^kn，我们可以将g’写成

同样根据对称性法则可以得到当p’ = 1/2时，g’取得最小值。

位数组的大小 

下面我们来看看，在不超过一定错误率的情况下，Bloom Filter至少需要多少位才能表示全集中任意n个元 素的集合。假设全集中共有u个元 

素，允许的最大错误率为є，下面 我们来求位数组的位数m。

假设X为全 集中任取n个元素的集合，F(X)是 表示X的位数组。那么对于集合X中任意 一个元素x，在s = F(X)中查询x都能得到肯定的结果，即s能够接 受x。显然，由于Bloom Filter引入了错误，s能够接 受的不仅仅是X中的元素，它还能够є (u - n)个false positive。

个集合。m位的位数组共有2^m个不同的组合，进而可以推出，m位的位 数组可以表示

个集合。全集中n个元素 的集合总共有

个，因此要让m位的位 数组能够表示所有n个元素的集合，必须有

即：

上式中的近似前提是n和єu相比很小，这也是实际情况中常常发生的。根据上式，我们得出结论：在错误率不大于є的情况下，m至少要 等于n log₂(1/є)才能表示任意n个元素 的集合。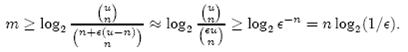

上一小节中我们曾算出当k = ln2· (m/n)时错误率f最小， 这时f = (1/2)^k = (1/2)^{mln2 / n}。现在令f≤є，可以推出

这个结果比前面我们算得的下界n log₂(1/є)大了log₂ e ≈ 1.44倍。这说明在哈希函数的个数取到最优时，要让错误率不超过є，m至少需要取到最小值的1.44倍。

总结： 

在计算机科学中，我们常常会碰到时间换空间或者空间换时间的情况， 即为了达到某一个方面的最优而牺牲另一个方面。Bloom Filter在时间空间这两个 因素之外又引入了另一个因素：错误率。在使用Bloom Filter判断一个元素是否 属于某个集合时，会有一定的错误率。也就是说，有可能把不属于这个集合的元素误认为属于这个集合（False Positive），但不会把属于这个集合的元素误认为不属于这个集合（False Negative）。在增加了错误率这个因素之后，Bloom Filter通过允许少量的错误来节省大量的存储空间。

自从Burton Bloom在70年代提出Bloom Filter之后，Bloom Filter就被广 泛用于拼写检查和数据库系统中。近一二十年，伴随着网络的普及和发展，Bloom Filter在网络领域获得了新生，各种Bloom Filter变种和新的应用不断出现。可以预见，随着网络应用的不断深入，新的变种和应用将会继续出现，Bloom Filter必将获得更大的发展。